התיאוריה המתמטית של מורכבות חושפת את הסתירה העמוקה של בינה מלאכותית – חוסר היכולת הבסיסית שלה להיות יצירתי באמת. מה ההבדל האמיתי בין מכונה וחשיבה אנושית? דווקא מאחורי נוסחאות מופשטות והבניות לוגיות עשויה התשובה להסתתר.
ישנן שלוש רמות של ידע: מה שאנחנו יודעים, מה שאנחנו יודעים אנחנו לא יודעים, ומה שאנחנו לא יודעים אנחנו לא יודעים. הקטגוריה האחרונה מציבה אתגר אמיתי לאינטליגנציה של מכונות, מכיוון שמחשבים אינם יכולים לחזות את הבלתי צפוי באמת.
תורת המורכבות קולמוגורוב היא גישה מתמטית למדידת תוכן המידע של עצמים, שהומצאה על ידי מתמטיקאי סובייטי בשנות ה-60. תארו לעצמכם שאתם צריכים לתאר אובייקט כלשהו בקצרה ככל האפשר, אך בצורה כזו שתשמר את כל מהותו. ככל שתיאור זה קצר ותמציתי יותר, כך "צפיפות המידע" של האובייקט גבוהה יותר.
לדוגמה, ניתן לתאר רצף של מיליון יחידות בפשטות רבה: "מיליון יחידות". ורצף אקראי של מיליון ספרות ידרוש תיאור הרבה יותר ארוך. קולמוגורוב הוכיח: ככל שקשה יותר לתאר אובייקט עם מספר מינימלי של סמלים, כך הוא ייחודי ובלתי צפוי יותר. מכונה לא יכולה לקבוע את הייחודיות הזו בעצמה כי היא דורשת מעבר לאלגוריתמים לוגיים.
המשפט המתמטי של גדל מצביע גם על המגבלות הבסיסיות של חשיבה מכונה. מחשב אינו יכול להעריך את היצירתיות שלו, משום שלכל תוכנה יש מגבלות לוגיות פנימיות: היא אינה מסוגלת ליצור אובייקט שנמצא לחלוטין מחוץ לתחום הקוד המקורי שלו.
אז, המוח האנושי שונה ממערכות אלגוריתמיות ביכולתו לייצר ידע חדש ביסודו. אנשים יכולים לתפוס באופן אינטואיטיבי הקשרים וקשרים שאינם ניתנים לפורמליזציה מתמטית. המכונה נידונה לפעול אך ורק במסגרת הכללים הנתונים.
הפתעה היא לא רק סטייה מהתבנית, אלא קפיצה איכותית בהבנת העולם. בינה מלאכותית משלבת מודלים קיימים ומקבצת מחדש מידע, אבל היא לא מסוגלת ליצור רעיון מהפכני באמת. בשביל יצירתיות אמיתית אתה צריך ללכת מעבר למבנים לוגיים.
המורכבות של אובייקט קשורה ישירות לייחודיות שלו. ככל שיש פחות כוח ניבוי, כך גדל פוטנציאל החידוש.
מערכות חכמות עובדות עם מודלים הסתברותיים, המתארות את המציאות הידועה בצורה מדויקת ככל האפשר. המוח האנושי מסוגל לעשות פריצות דרך אינטואיטיביות, לייצר מושגים שלא ניתן להסיק מנתונים זמינים באמצעות שרשרת לוגית פשוטה.
עם זאת, המגבלות של אינטליגנציה מכונה אינן גורעות מחשיבותה. להיפך, הם מדגישים את העומק והרבגוניות של המחשבה שלנו.
פילוסופים ומתמטיקאים ממשיכים לחקור את הגבול הדק שבין חשיבה אלגוריתמית ליצירתית. תיאוריית המורכבות פותחת אופקים חדשים להבנת טבעה של אינטליגנציה, ומדגימה את טבעה הרב-שכבתי ואת חוסר ההתכלות הבסיסי שלה.
קבוצת חוקרים הונגרים בראשות מתמטיקאי
גאבור דומוקושה
גילה תגלית שיכולה לשנות את רעיון הגיאומטריה, הטבע והאמנות. הם גילו סוג חדש של צורות גיאומטריות הנקראות "תאים רכים" שיכולים למלא לחלוטין מישורים וחללים תלת מימדיים. הייחודיות של צורות אלה נעוצה בהיעדר זוויות: בדו מימד, לתאים כאלה יש רק שתי פינות המחוברות בקימורים, ובתלת מימד אין להם פינות כלל.
העבודה החלה
בניסיון לענות על השאלה, מהו המספר המינימלי של זוויות שיכולה להיות לדמות שיכולה לרצף מישור ללא פערים. חוקרים מצאו שהמספר המינימלי הוא שניים. זה סותר את האמונות שהיו בעבר לפיהן ריצוף אינו אפשרי ללא דמויות בעלות שלוש פינות, כגון משולשים. מחקר נוסף הוביל לפיתוח של אלגוריתם מתמטי שאיפשר להפוך פוליהדרות קלאסיות לצורות רכות מעוגלות. אלגוריתם זה מבוסס על תורת הגרפים, כלומר נתיבים המילטון, שאפשרו להחליק את פינות הפוליהדרות ולהפוך אותן לסוגים חדשים של תאים.
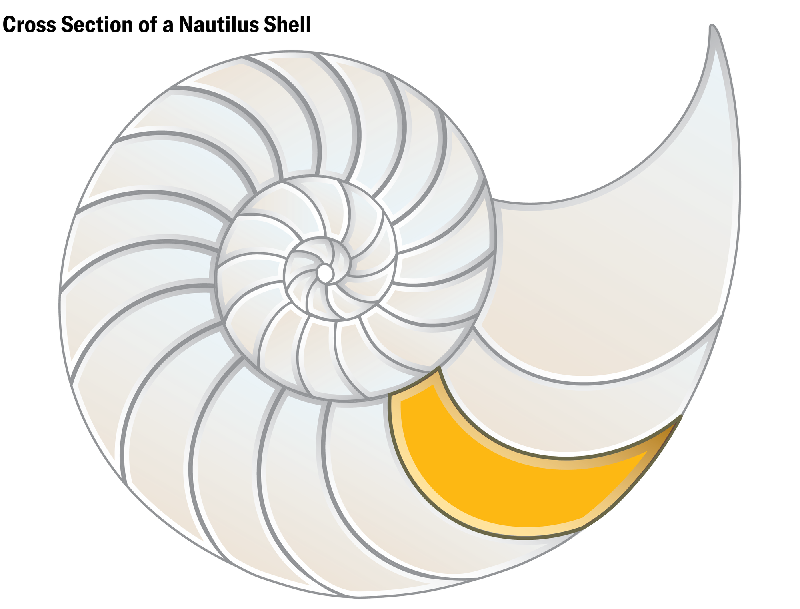
התברר שתאים רכים הם יותר מסתם תופעה מתמטית. מדענים החלו למצוא צורות כאלה בטבע, באמנות ובאדריכלות. במיוחד גילו חוקרים מבנים דומים בקונכיות של נאוטילוסים ואמוניטים. לצורות טבעיות אלה יש צריכת אנרגיה מינימלית בשל היעדר פינות חדות. באורגניזמים חיים, תאים רכים מספקים מילוי שטח יעיל, שניתן לראות ברקמות, בתאי דם ובמבנים אחרים. באדריכלות, צורות דומות שימשו בעיצובים של זאהה חדיד ואדריכלים אחרים שעבדו עם קווים זורמים ואורגניים.
עבודתם של החוקרים ההונגרים נגעה גם בקשר שבין הטבע לחפצים מעשה ידי אדם. התברר שהמושג של תאים רכים כבר יושם באופן אינטואיטיבי בפרויקטים אדריכליים. לדוגמה, תכנון הבניין של Cirque du Soleil השתמש באלמנטים התואמים מתמטית לתאים רכים. ממצא זה מפגיש בין אמנות, מדע ועיצוב, ומראה שצורה אורגנית יכולה להיות פתרון אסתטי ופונקציונלי כאחד.
המחקר לא הוגבל לתאים דו מימדיים. דומוקוס ועמיתיו הוכיחו את קיומם של תאים רכים תלת מימדיים שיכולים למלא חלל ללא פינות. הם מצאו דוגמאות לצורות כאלה בטבע וגם פיתחו אלגוריתמים ליצירתן. צורות אלו משלבות נזילות של קו ויכולת למלא נפח ביעילות, מה שפותח אפשרויות חדשות עבור מדעי החומרים, אדריכלות וביולוגיה.

עבודתם של החוקרים מעלה שאלות חדשות רבות. לדוגמה, האם ניתן ליצור תאים רכים שיכולים למלא חלל מבלי לחזור על דפוסים, כפי שקורה עם
פסיפסים א-מחזוריים
? המחקר עוסק גם בנושא מילוי חלל מיטבי במבנים ביולוגיים וחומרים מלאכותיים. למרות שעדיין לא קיימות עדויות ישירות לתהליכים ביולוגיים הקשורים לתאים רכים, התאמות חזותיות עם מבנים טבעיים מצביעות על הבטחה בתחום זה.
חקר התאים הרכים כבר משך את תשומת לבם של מדענים מתחומים שונים. הוא משלב גיאומטריה, ביולוגיה ואמנות, ומציע גישות חדשות לחקר החלל והמבנה שלו. התגלית מדגישה כיצד הטבע נמנע מקצוות חדים, בוחר בצורות חלקות וחסכוניות יותר באנרגיה. הכיוון הזה מבטיח להפוך לבסיס לטכנולוגיות ותיאוריות חדשות שיעזרו להבין את מבנה העולם סביבנו.
אלכסנדר אנטיפוב
קישור למקור